- ... (1930)1
- actually Bloch (1929) came with it first,
but Dirac is popularly blamed.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
components2
- Please, excuse my notation here. I use ``hats'' above operators/potentials (e.g.,
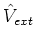 is the external potential)
and no ``hats'' above the corresponding energy components (e.g.
is the external potential)
and no ``hats'' above the corresponding energy components (e.g. 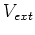 is the energy corresponding to
external potential). The exception is a hamiltonian for which
is the energy corresponding to
external potential). The exception is a hamiltonian for which 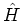 is the operator, while
is the operator, while
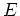 is the value of energy. This may add confusion, since in much of the literature energy components
are denoted with capital letters or subscripted
is the value of energy. This may add confusion, since in much of the literature energy components
are denoted with capital letters or subscripted 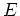 's, while the operators are in capital letters, and
potentials in lowercase letters. But this notation also leads to a conflict with notation for one-particle
operators, which are written often in lower case.
's, while the operators are in capital letters, and
potentials in lowercase letters. But this notation also leads to a conflict with notation for one-particle
operators, which are written often in lower case.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
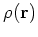 3
3
- actually,
in the original HK paper, and many papers with a physical slant, the density is denoted as
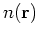 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... optimized4
-
it also needs to be constrained by v-representability, but
we still do not know how to express v-representability in a closed
mathematical form. There exist, however, methods, e.g.,
constrained search (Levy, 1982) and local-scaling
transformation (Petkov et al, 1986) which assure v-representability
during density optimization, though their algorithmic implementation
needs to be done.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... equation5
- if expansion into basis sets is used,
the matrix equation (57) for expansion coefficients is identical as
in Hartree-Fock method.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... field6
- It has to be stressed that
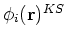 's are not the real orbitals, and
they do not correspond to a real physical system. Their only role in the theory is to
provide a mapping between kinetic energy and density. For one, the total KS wave function is a single determinant
and is unable to model situations where more determinants are needed to describe the system (e.g., for
cases when molecules dissociate to atoms). Interesting discussion about the symmetry of this wave
function is given by Dunlap (1991, 1994). More studies are needed to asses physical relevance of these orbitals.
's are not the real orbitals, and
they do not correspond to a real physical system. Their only role in the theory is to
provide a mapping between kinetic energy and density. For one, the total KS wave function is a single determinant
and is unable to model situations where more determinants are needed to describe the system (e.g., for
cases when molecules dissociate to atoms). Interesting discussion about the symmetry of this wave
function is given by Dunlap (1991, 1994). More studies are needed to asses physical relevance of these orbitals.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
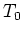 7
7
-
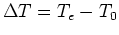 is embedded in
is embedded in 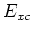 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.