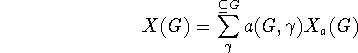
D. J. Klein
Chemical Sub-Structural Cluster Expansions for Molecular Properties
Texas A&M University at Galveston, Galveston, Texas 77553-1675
The correlation of different molecular sub-structures with various molecular properties has a long history, of over a century, and it still remains of current (perhaps even central) interest in chemistry. E.g., this interest is manifested in the focus on ``functional groups'' in organic chemistry, particularly in connection with reactivities. An example in physical chemistry concerns the use of bond energy or ``group function'' methods to empirically express thermodynamic heats of atomization, though several other properties are often similarly treated. And there are many other examples of such sub-structural analysis. Here a general systematic way to expand rather general properties in terms of molecular sub-structures is described. The most classical such expansion starts with atomic contributions for each type of atom in a molecule, and then incorporates contributions for each type of chemical bond, and after this neighbor bond-pair contributions may be included, and in principle even further larger substructural units may be considered. For example, in expanding enthalpies such contributions may be simply added together. Formally a general type of cluster expansion for a property X taking the value X(G) for structure (or graph) G may be presented thusly
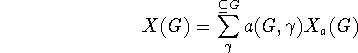
where the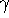 
-sum is over a suitable set of substructures of G, 
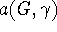is X-independent depending
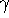solely on the manner in which embedds in G, and the parametric coefficient 
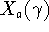is G-independent depending on the property X as well as the type of cluster expansion implemented.
As a simple example, 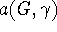may be 1 or 0 for each specific set of atoms of G depending whether
they are connected or not in the substructure gamma in G (e.g., as two particular atoms are connected
or not by a bond, and the next higher sub-structures would be triples of atoms with two of them
each connected to the third). Quite often the expansion is rephrased in terms of equivalence
classes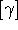 
of structures, whence
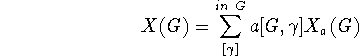
where the sum is now over these equivalence classses, and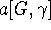 
is a sum over 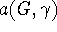for all the
particular substructures which are so equivalent in G. In our proto-examplar case 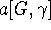then
becomes the number of sub-structures of the given type in G (e.g., the number of C-C bonds in
G, and in the next higher order the number of C-C-C units). It is emphasized that cluster
expansions may be made in a systematic manner including ever larger connected substructures to
attain ever higher precision, and different approaches to the choice of the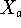 
-coefficients may be
made. Within the general cluster- expansion formalism there can be:
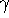different
choices for 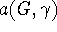can be made, e.g., for 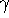the i 
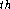& j 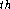atoms which are
connected by a C-C bond
one could take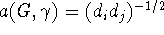 
with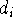 
& 
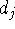the degrees of atoms i & j in the C-network);
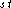and 3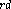 
of these C atoms are also directly connected, and
allowing their contribution to be subsumed in a separate term for 3 mutually interconnected C
atoms);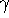 -sums in the two displayed equations as being over disconnected spanning graphs in G,
possibly with one of the components distinguished).
Though many authors have discussed cluster-expansion ideas in varying degrees of generality, an outline of the current general formalism is found in ref. [1].
Some differing aspects of making an expansion may be motivated by the particular property under consideration. The rather broad categorization of each property as ``additively'', ``constantively'', ``multipicatively'', or ``derivatively'' bounded is made - and the inter-relations between and utility of this categorization is noted in motivating the manner of combination of the substructural contributions in a cluster expansion.
A wide range of example applications are possible and some may be noted. These include the cluster expansion of: energies, magnetic susceptibilities, boiling points, NO- bioactivities, statistical-mechanical partition functions, quantum-mechanical wave-functions, and model Hamiltonians. Schemes for the choice of the parameters appearing in the expansions are indicated: via least-squares fitting of all data available (whence an optimal data-set-dependent fit is obtained); via ``Möbius'' inversion (whence a data-set-independent fit is enforced); or via an intermediate ``balanced'' scheme. Example applications are found in refs. [2] , [3], & [4]. Overall the cluster-expansion approach can be advocated as a general method not only to analyze a a molecular structure in terms of its substructures, but more generally to analyze a ``whole''in terms of its ``parts''.
Back to Program PageBack to Main Page