The surface and volume of a molecule have a clearly conventional character. A molecule is a system of moving particles (nuclei and electrons) which are held together by forces electrostatic and magnetic in nature, and as such does not posses any definitive boundaries. However, representing a molecule as a solid figure, as we will see, is a very useful chemical concept and has proved its utility in medicinal chemistry. Also, it is not surprising that it has a strong scientific justification in the form of intermolecular forces which will be discussed later in this chapter.
Figure 6.14: Van der Waals surface of acetic acid.
It was observed long ago that two atoms which are not covalently bound
cannot approach each other closer than a certain minimal distance even in
tightly packed molecules or molecular assemblies (e.g. crystals). The closest
proximity depends upon the type of atoms involved. This
phenomenon can be described by assigning a value called a van der Waals
radius,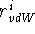 
, to each atom type in such a way that the sum of these
quantities for a given atom pair, i and j, is equal to their closest
possible distance:
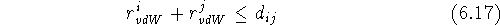
Obviously, it is an approximation, and hence, many different tables of ``best'' van der Waals radii exist, even though the values for corresponding atoms coming from different authors are similar. In geometric terms, the van der Waals radius can be imagined as a spherical ``shield'' surrounding the atom, and the closest distance between two non-bonded atoms is when their respective shields touch. However, the shields of covalently bonded atoms intersect since bond lengths are much shorter than the sum of the van der Waals radii partaking atoms. A molecular van der Waals surface, also called a van der Waals envelope, is composed of the spheres for individual atoms with their intersecting sections removed (Fig. 6.14).
For a single molecule (i.e., molecule for which there is a path
between any two atoms along
covalent bonds), the van der Waals envelope
is a closed surface, and hence, it contains volume. This volume is called
the molecular volume, or van der Waals volume and is usually given in Å 
.
The straightforward way of calculating molecular volume on the
computer is by numerical
integration, i.e., by surrounding the van der Waals envelope with a grid
of small bricks and summing up the bricks whose centers are within the
van der Waals envelope of the molecule (i.e., are within a van der Waals
radius from atom nucleus). This is illustrated in Fig. 6.15 where the
size of bricks is intentionally exaggerated to show the concept of
numerical integration.
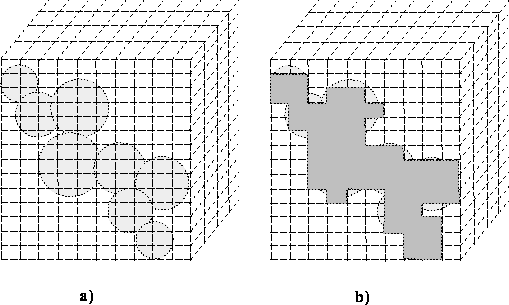
Figure: Numerical integration of molecular volume: a) the van der Waals
envelope on the grid, b) bricks included for integration.
With large bricks there is a substantial error in calculations, however accuracy is obtained by using smaller bricks at the expense of computer time. There are also algorithms faster than numerical integration that are based on analytical solutions to the volume of intersecting spheres.
Molecular volume of a single molecule has a limited value, though it is used sometimes as a molecular index in QSAR equations since it correlates strongly with molar refraction (MR) and can serve as a theoretically derived substitute for this parameter. Molecular volume can also be employed as a measure of molecular similarity and help in understanding the steric requirements of a receptor. Modeling systems usually incorporate facilities to operate on molecular volumes and display the results graphically.
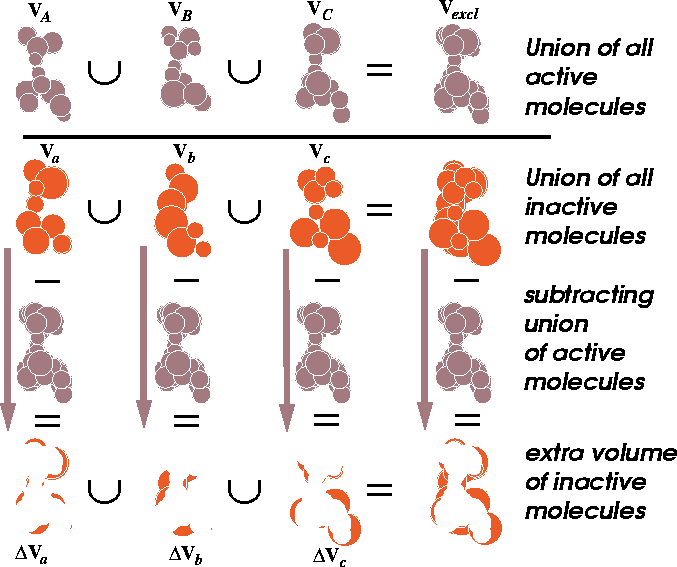
Figure 6.16: Illustration of union and difference of molecular volumes.
The volume union of active molecules
is depicted at the top. In the next row, the union of inactive molecules
is represented. The extra volume (a difference between the volume of
inactive molecule and the union of all active molecules) is illustrated
at the bottom row.
Let us assume that we have two molecules, A and B and we want to find out how similar their shapes are. As the first step, the two molecules, A and B, have to be superimposed. The alignment rules depend upon the features we want to compare, e.g., we might superimpose their backbones or their pharmacophoric groups. Molecular modeling systems offer a variety of methods for superimposing molecules which will be described later in this chapter. We can calculate the union of two or more volumes by counting bricks whose centers are within the envelope of at least one molecule:
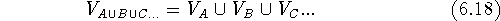
where 
is a mathematical symbol for the union of sets.
This operation does not depend upon the order in which the
volume maps are taken.
The union of molecular volumes of a series of active drug molecules
(assuming that they are properly superimposed,
that they are taken with their receptor bound geometry, and that the receptor
does not undergo conformational change on binding) represents the
approximate shape of the receptor cavity and is called the excluded
volume,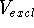 
(Marshall et al., 1979). More precisely
,
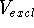is a volume not protruded by the receptor. Since our series of active
molecules is limited in number and shape, we may never be sure if our set
spans the whole cavity of the receptor.
Volumes can also be subtracted,
in which case, only those bricks are counted which are within the envelope of
molecule A, but not within the envelope of B:
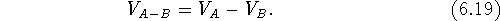
This operation can only be performed on two volume maps and its
result depends upon the order (i.e.,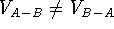 
).
The intersection of two or more volumes
consists only of bricks which are simultaneously within the
van der Waals envelopes of all molecules:
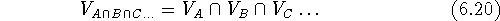
where 
is a symbol for intersection of sets. The intersection
does not depend upon the order of maps.
If we have a series of inactive drug analogs, a, b, c ...,
we can subtract the excluded volume, 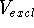, from their volume
maps and find those portions
of their volume maps which did not appear in any of the active molecules:
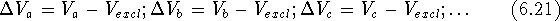
Now, by calculating the intersection of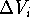 
's we can find a volume
which was present in each of the inactive molecules but was not present
in any of the active molecules. This volume is called the receptor
essential volume:
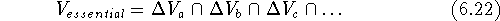
This volume map may represent a steric hindrance which prevents the inactive analogs from interacting efficiently with the receptor (Klunk et al., 1983). This volume, however, may be empty if each low-activity analog was probing a different portion of the receptor wall. For such a case, there is a variant of this scheme when the union of the volumes of active molecules is subtracted from the union of inactive molecules. We assume here that the additional volume present in inactive molecules has a detrimental impact on activity due to steric hindrance within the receptor cavity. Some operations on molecular volumes are represented in Fig. 6.16.
When analyzing the molecular volume, it is important to remember that volume is not the only factor in the ligand-receptor interaction. The ligand molecule must be able to approach the receptor before the binding can take place. Assuming that it can be transported to its place of action, the long range electrostatic forces are needed to drive the ligand toward the receptor. Volume represents only the contribution from the short range van der Waals interactions and is important when the receptor and ligand are at close proximity. However, other forces (e.g., electrostatic repulsion), lack of specific interactions (e.g., formation of hydrogen bonds between ligand and receptor), and unfavorable entropic contributions, may prevent efficient binding even if ligand and receptor shapes are complementary.
Theoretically derived molecular shape descriptors (MSD), based on
operations on molecular volumes, are also used in QSAR. In this case,
the most active molecule of the series (i.e., the molecule which
most likely fits the receptor best) is taken as a reference molecule, r,
and other molecules (compared molecules, i) are superimposed onto it.
The numerical value of the intersection of the molecular volume of
molecule, r, and molecule i is called
the overlapping volume, 
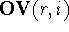, while the numerical
value of the difference between volume maps of i and r (i.e., the volume of
the molecule i not shared with molecule r) is called
the non-overlapping volume,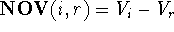 
(Motoc et al., 1985). Note that 
,
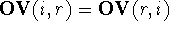but 
.
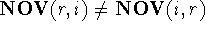These values, together with other parameters, may be used in QSAR equations
to explain factors affecting the biological activity of the molecule.
Also, the complementarity of the shape of the
drug molecule and the receptor cavity is important
for selectivity. For these reasons molecular volume plays a central
role in computer-aided drug design.
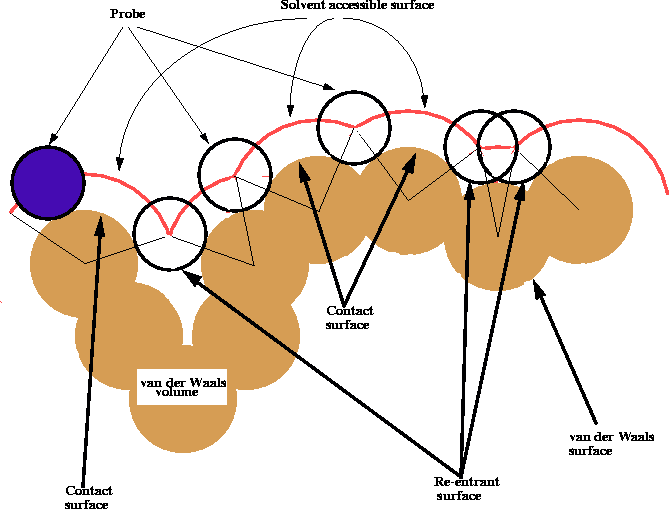
Figure 6.17: Calculation of the solvent accessible
surface of a molecule.
The shape of the van der Waals surface of a molecule may be misleading, especially for macromolecules, since it frequently contains small gaps, pockets and clefts which are sometimes too small to be penetrated even by a solvent molecule like water. For all practical purposes, the van der Waals surface of these oddments cannot enter into contact with a solvent or a drug molecule and therefore is not truly an accessible surface. To ``smooth'' the roughness of the van der Waals surface, Richards (1977) introduced the concept of a contact surface and a solvent accessible surface. These surfaces are obtained by rolling a spherical probe of a diameter corresponding to the size of a solvent molecule (usually water) on the original van der Walls surface (Fig. 6.17). As a result, the area where the probe touches the van der Waals surface is called the contact surface, the center of the spherical probe traces a surface called the solvent accessible surface and the patches over narrow gaps and clefts traced by the surface of the probe are called re-entrant surfaces. An efficient computer algorithm for deriving these surfaces was described by Connolly (1983). For a good discussion of the topic of molecular surface and its use consult Dean (1987).
The exploration of molecular volume and surface is essential for the understanding of drug action since short range dispersion forces play a major role in the binding of drug molecules to receptors. For efficient and specific binding, the receptor cavity, in most cases, must be tightly filled with the interacting ligand. On the other hand, when walls of the receptor cavity are rigid, even a small extra volume in the ligand prevents efficient binding and renders the molecule inactive. The surfaces of interacting molecules also need to be of complementary character, i.e., they should both be hydrophobic or hydrophilic which will in practice represent their ability to form hydrogen bonds. The net charge on the interacting surfaces also needs to be complementary for strong bonding. To aid in this analysis, advanced molecular modeling systems allow ``painting'' of the surface of the molecule according to electrostatic potential or the presence of polar/apolar groups, etc. The exploration of molecular volume and surface is frequently the first and most important step on the path to understanding the molecular basis of drug-receptor interactions.