

Next: Molecular Mechanics
Up: Molecular Modeling
Previous: Types of molecular images
Molecular modeling raison d'être is to perform computer
simulations, or to do chemical experiments with a computer
rather than a laboratory bench. Though the results of such simulations
have to be validated by experiment, it is known that in many cases we
may rely on them as much as on the true experimental values. On many
occasions calculations showed flaws in original experimental data and
led to corrected experiments which agreed with the theory. Simulation
requires a model, a mathematical description of a system to be
simulated. It is important to accept that the particular model need not
be ``real'', but good models usually have a sound
scientific justification to yield useful results.
This section briefly outlines potential energy functions used in
molecular mechanics and dynamics methods.
Intelligent use of these methods requires more information than can be
given here. An excellent monograph on this topic by
Burkert & Allinger (1982) is available. Also the actual software instructions
accompanying molecular modeling systems describe the terms in great
detail.
There are in general two approaches to molecular simulation: quantum
methods, and empirical methods. Quantum methods are based on principles
of quantum mechanics. The most rigorous implementations of quantum
formalism, called ab initio methods, do not
require and experimental data, beside a handful of basic physical
constants like: speed of light, electron mass, elementary charge, etc.
The empirical methods reviewed in this
section derive their origin from classical chemical concepts and
are based for the most part on experimental observations.
This does not mean
however that they do not use quantum results and procedures. In fact
there are numerous examples of combination, quantum/empirical approaches,
where some parts of a system are treated quantum mechanically and
others are described by classical mechanics. The boundary between
these methods becomes more and more blurred with time.
It is well known from structural chemistry and from quantum calculations
that bond lengths and
valence angles in typical units and groups are very similar even if they
appear in different molecules. The single bond between two sp  hybridized
carbon atoms is around 1.5 Å long and the valence angle for an
sp3 carbon is
usually close to 109
hybridized
carbon atoms is around 1.5 Å long and the valence angle for an
sp3 carbon is
usually close to 109  . On the other hand, these values are frequently
distorted in some strained ring systems (like cyclopropane) or
crowded molecules (like tetramethylmethane). The concept of molecular
strain can be imagined as if bonds were elastic springs whose distortion
is reflected by a positive increment (i.e., thermodynamically
unfavorable) to the potential energy of the molecule.
These approaches were originally called empirical potential energy
functions but the term molecular mechanics is now in common use.
The mathematical form of this
potential energy function (also called potential energy surface) is:
. On the other hand, these values are frequently
distorted in some strained ring systems (like cyclopropane) or
crowded molecules (like tetramethylmethane). The concept of molecular
strain can be imagined as if bonds were elastic springs whose distortion
is reflected by a positive increment (i.e., thermodynamically
unfavorable) to the potential energy of the molecule.
These approaches were originally called empirical potential energy
functions but the term molecular mechanics is now in common use.
The mathematical form of this
potential energy function (also called potential energy surface) is:
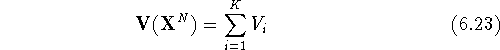
where 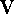 represents the potential
energy of the molecular system and depends upon the cartesian coordinates
of all atoms denoted here as
represents the potential
energy of the molecular system and depends upon the cartesian coordinates
of all atoms denoted here as 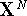 .
. 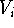 's are individual energy terms
representing contributions from individual interactions which
depend upon the cartesian coordinates of partaking atoms.
Having
's are individual energy terms
representing contributions from individual interactions which
depend upon the cartesian coordinates of partaking atoms.
Having 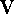 we can calculate the potential energy of the molecular
system as well as the forces acting on atoms and groups. Individual
energy terms,
we can calculate the potential energy of the molecular
system as well as the forces acting on atoms and groups. Individual
energy terms, 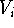 , are functions of coordinates (usually internal
coordinates)
and parameters, i.e., constants, called force field parameters.
The set of such parameters and the functional form of these terms is called
a force field. In a good force field, parameters are well
balanced and produce consistent results. On the other hand,
there are many different force fields which differ
substantially in the values of corresponding parameters and
in the functional form of the energy terms.
, are functions of coordinates (usually internal
coordinates)
and parameters, i.e., constants, called force field parameters.
The set of such parameters and the functional form of these terms is called
a force field. In a good force field, parameters are well
balanced and produce consistent results. On the other hand,
there are many different force fields which differ
substantially in the values of corresponding parameters and
in the functional form of the energy terms.
Merging parameters from
different force fields is therefore discouraged.
While the internal coordinates can easily be
calculated from the cartesian coordinates of the atoms
of the actual molecule, the parameters entering into the
energy function must be known in advance for all types of atoms comprising
the molecular system. As will become clear from the following discussion, many
parameters are needed to describe even simple biological molecules.
For some more exotic atom types, such parameter are still not available.
You can always put some number
in place of the missing force field parameter, however, your results will be
as reliable as these parameter values. There is a growing tendency to
estimate needed force field parameters from ab initio quantum
calculations, by performing such calculations on small, model molecules
assuming that the results are transferable to larger molecules. This approach
has the added advantage that calculations can be performed for all, even
non-existing species, while reliable experimental data are only available
for the most popular molecules.
Individual terms 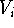 can be grouped into three classes:
can be grouped into three classes:
- Bonded terms -- describe contributions from atoms which are
covalently bound. They include bond stretching, angle bending, out-of-plane
distorsions, and torsional terms. Some force fields include cross-terms,
e.g., stretch-stretch, stretch-bend, etc.
- Non-bonded terms -- represent contributions to potential
energy coming from interactions which atoms which are not covalently bound,
i.e., van der Waals interactions, electrostatic interactions
and hydrogen bonds.
- Constraints -- artificial terms incorporating
existing knowledge (e.g., structural information from NMR) or used to test
structural hypotheses.
The bond stretching term, 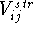 , for a covalent bond between atoms
i and j, represents a contribution to the potential energy
resulting from deformation of the optimal bond length. Most frequently a simple
symmetric parabola (i.e., harmonic approximation) is used:
, for a covalent bond between atoms
i and j, represents a contribution to the potential energy
resulting from deformation of the optimal bond length. Most frequently a simple
symmetric parabola (i.e., harmonic approximation) is used:
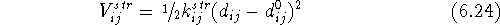
where 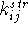 is a bond stretching parameter (frequently called
a bond stretching force constant) and its value represents the stiffness
of the bond (i.e., the ease with which the bond can be distorted). Large
values of
is a bond stretching parameter (frequently called
a bond stretching force constant) and its value represents the stiffness
of the bond (i.e., the ease with which the bond can be distorted). Large
values of 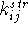 correspond to ``hard'' bonds and small values
to ``soft'' bonds.
The value of
correspond to ``hard'' bonds and small values
to ``soft'' bonds.
The value of 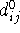 corresponds
to the optimal (i.e., unstrained) bond length. Contribution
from this term is never negative and is equal to zero only when the actual bond
length,
corresponds
to the optimal (i.e., unstrained) bond length. Contribution
from this term is never negative and is equal to zero only when the actual bond
length, 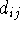 , is exactly equal to the optimal bond length
, is exactly equal to the optimal bond length 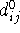 .
The actual
bond length
.
The actual
bond length 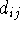 is calculated from the cartesian coordinates of atoms
i and j as in eq. 6.14. For accurate calculations more elaborate
expressions for the bond stretching term are used, e.g., a Morse potential,
which takes into
account the fact that the potential for bond deformation is not symmetric
and it is easier to stretch the bond than to squeeze it.
is calculated from the cartesian coordinates of atoms
i and j as in eq. 6.14. For accurate calculations more elaborate
expressions for the bond stretching term are used, e.g., a Morse potential,
which takes into
account the fact that the potential for bond deformation is not symmetric
and it is easier to stretch the bond than to squeeze it.
The form of the angle bending term is very similar. In most cases the
contribution to potential energy, 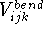 , is represented by a
harmonic expression depending upon the bending force constant,
, is represented by a
harmonic expression depending upon the bending force constant,
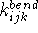 , the actual value of the valence angle
, the actual value of the valence angle 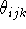 and its
``natural'', optimal value,
and its
``natural'', optimal value, 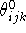 :
:
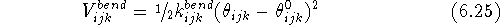
The out-of-plane term is used to account for the energy contribution from
distorting an aromatic or conjugated system of bonds from planarity and
is most frequently a harmonic term:
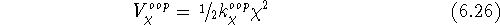
where in the case of sp  hybridized carbon,
hybridized carbon, 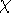 is an angle between
one of the bonds originating at the central atom and a plane passing through
the other two bonds.
is an angle between
one of the bonds originating at the central atom and a plane passing through
the other two bonds.
The functional form of the torsional term is unique.
In most cases, it depends on the cosine of the product of
a torsional angle and the periodicity (see Fig. 6.21):
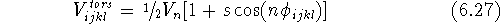
where 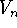 is the height of the torsional barrier; s is -1 if a minimum
occurs for the eclipsed conformation and +1 if a minimum corresponds to
the staggered conformation; n is a periodicity, i.e., the number of maxima
per full revolution; and
is the height of the torsional barrier; s is -1 if a minimum
occurs for the eclipsed conformation and +1 if a minimum corresponds to
the staggered conformation; n is a periodicity, i.e., the number of maxima
per full revolution; and 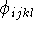 is a torsional angle.
For the torsional angle involving C--C bond in ethane, s=1 and n=3, while
for the double bond in ethylene s=-1 and n=2. More elaborate
force fields use as a torsional term the sum of several cosine functions
with different periodicities to account for smaller ``humps'' appearing
on the torsional energy dependence. On occasion, the harmonic potential
is used for torsional angles around double bonds due to their stiffness.
is a torsional angle.
For the torsional angle involving C--C bond in ethane, s=1 and n=3, while
for the double bond in ethylene s=-1 and n=2. More elaborate
force fields use as a torsional term the sum of several cosine functions
with different periodicities to account for smaller ``humps'' appearing
on the torsional energy dependence. On occasion, the harmonic potential
is used for torsional angles around double bonds due to their stiffness.
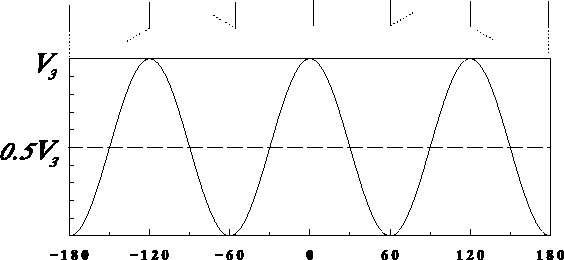
Figure 6.21: Plot of torsional energy dependence upon the torsional angle:
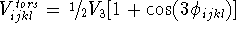 .
.
Non-bonded terms describe contributions brought by the interaction of atoms
which are not covalently bonded. Moreover, atoms which are two bonds apart
(1-3 interactions), are usually not included in the
non-bonded interaction list, since
it is assumed that their interaction is satisfactorily accounted for by
the angle bending term.
However, non-bonded interactions of atoms separated by
3 covalent bonds in the molecular graph (1-4 interactions) are
routinely included in spite
of the fact that they appear in the torsional term, though
their magnitude is frequently scaled by 50%.
Generally, the non-bonded interactions
represent contributions to energy from van der Waals interactions,
electrostatic interactions and they frequently account explicitly for hydrogen
bonds. There are many expressions for these terms and only the
simplest ones will be described here to illustrate the underlying ideas.
The non-bonded terms are usually represented mathematicaly
as two-body interactions. They depend on the coordinates of only two
interacting atoms, i.e., are represented as pairwise potentials.
This is an approximation,
and it is well known that the interaction between two atoms depends
significantly upon the positions of other atoms, especially those at close
proximity. However, even for pairwise potentials, calculation of
non-bonded terms is at present
a significant computational effort proportional to the square in
number of atoms. For three-body potentials (i.e., functions which
depend on positions of three non-bonded atoms), this effort is
proportional to the cube in number of atoms and unmanageable for larger
molecules. For example, for a small sizes protein containing 1000 atoms,
there are roughly 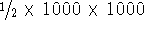 pairwise
interactions,
or
pairwise
interactions,
or 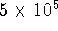 terms. The
terms. The 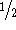 factor
comes from the fact that each pair is included only once, i.e., the pair
i--j is equivalent to j--i. For the three-body potentials
we would have to calculate interaction for each possible combination of
three atoms (excluding valence angles), i.e., close to
factor
comes from the fact that each pair is included only once, i.e., the pair
i--j is equivalent to j--i. For the three-body potentials
we would have to calculate interaction for each possible combination of
three atoms (excluding valence angles), i.e., close to
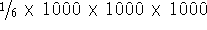 or
or
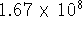 terms! For that reason, the three-body potentials
are not routinely calculated. However, even two-body potentials are
computationally demanding and approximations are used.
The large number of terms is frequently
reduced by omitting the
interactions of distant atoms (i.e., skipping calculation
of the non-bonded term for atoms which are further apart than some
predetermined
cut off distance). However, checking if atoms are outside the cut off distance
is also a substantial computational effort for larger molecules.
terms! For that reason, the three-body potentials
are not routinely calculated. However, even two-body potentials are
computationally demanding and approximations are used.
The large number of terms is frequently
reduced by omitting the
interactions of distant atoms (i.e., skipping calculation
of the non-bonded term for atoms which are further apart than some
predetermined
cut off distance). However, checking if atoms are outside the cut off distance
is also a substantial computational effort for larger molecules.
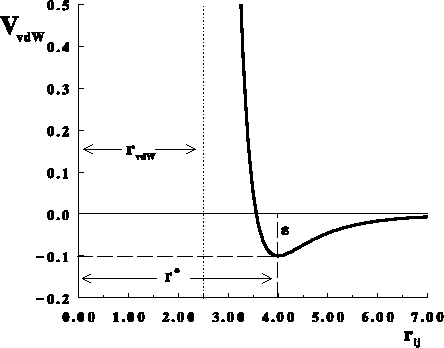
Figure: Dependence of van der Waals energy upon distance between
two atoms approximated by a Lennard-Jones 12-6 potential (eq. 6.29).
Here: m=6, n=12, 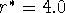 Å,
Å, 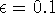 kcal/mol,
kcal/mol,
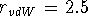 Å
Å
The van der Waals interaction energy, 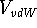 , is composed
of two terms opposing each another, a repulsive term
, is composed
of two terms opposing each another, a repulsive term 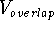 , and
an attractive term,
, and
an attractive term, 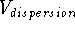 :
:
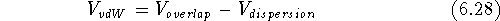
The repulsive term, 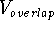 , rapidly grows at close interatomic distances
due to the overlapping of the electron clouds of the two atoms which results
in the disruption of their electronic structure. This leads to the exposing of
their nuclei and gives rise to a strong repulsion of positive charges.
At moderate distances between atoms, i.e., larger than the sum of their
van der Waals radii, the dispersion term,
, rapidly grows at close interatomic distances
due to the overlapping of the electron clouds of the two atoms which results
in the disruption of their electronic structure. This leads to the exposing of
their nuclei and gives rise to a strong repulsion of positive charges.
At moderate distances between atoms, i.e., larger than the sum of their
van der Waals radii, the dispersion term, 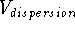 , dominates. These
attractive forces were first identified by London in 1930, and
exist even when molecules have no permanent charge or dipole moment.
The dispersion energy is of quantum mechanical origin and cannot be
completely described in classical terms. The electrons in an atom are
in continuous motion and the electron distribution around the nucleus is
constantly fluctuating giving rise to instantaneous dipole moments.
Though on the average the dipole moment of an atom is zero,
at any given moment there is some temporary dipole moment present
which by induction produces a dipole moment of opposing direction in the
neighboring atom. The attraction of these instantaneous dipoles results in
a dispersion energy. The simplest and most widely used equation
approximating this behavior is due to Lennard-Jones.
It is illustrated in Fig. 6.22 for two atoms i and j
as a function of their distance
, dominates. These
attractive forces were first identified by London in 1930, and
exist even when molecules have no permanent charge or dipole moment.
The dispersion energy is of quantum mechanical origin and cannot be
completely described in classical terms. The electrons in an atom are
in continuous motion and the electron distribution around the nucleus is
constantly fluctuating giving rise to instantaneous dipole moments.
Though on the average the dipole moment of an atom is zero,
at any given moment there is some temporary dipole moment present
which by induction produces a dipole moment of opposing direction in the
neighboring atom. The attraction of these instantaneous dipoles results in
a dispersion energy. The simplest and most widely used equation
approximating this behavior is due to Lennard-Jones.
It is illustrated in Fig. 6.22 for two atoms i and j
as a function of their distance 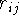 :
:
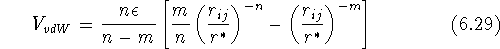
where  is the depth of a well (i.e., the maximal attraction energy),
n and m are exponents (typically n=12 or 9, and m=6),
and
is the depth of a well (i.e., the maximal attraction energy),
n and m are exponents (typically n=12 or 9, and m=6),
and 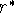 is the distance between atoms which corresponds to a minimum.
As you can see from Fig. 6.22, the curve climbs abruptly to large values
for distances
just below the optimal distance
is the distance between atoms which corresponds to a minimum.
As you can see from Fig. 6.22, the curve climbs abruptly to large values
for distances
just below the optimal distance 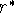 . At some distance, the repulsion energy
is so large that further approach of atoms is no longer possible. This
interatomic distance corresponds to the sum of the
van der Waals radii of two atoms,
i.e., the van der Waals surface has a strong justification in the
form of interatomic forces. On the other side of the minimum, the dispersion
energy decays rapidly with distance. Bear in mind, however, that for atoms
buried in the center of a large molecule, the number of these distant
interactions grows rapidly with distance (because you can place more atoms
on the surface of the larger sphere), and the sum of all these minute
interactions decays at a slower rate than for the isolated two-atom case.
. At some distance, the repulsion energy
is so large that further approach of atoms is no longer possible. This
interatomic distance corresponds to the sum of the
van der Waals radii of two atoms,
i.e., the van der Waals surface has a strong justification in the
form of interatomic forces. On the other side of the minimum, the dispersion
energy decays rapidly with distance. Bear in mind, however, that for atoms
buried in the center of a large molecule, the number of these distant
interactions grows rapidly with distance (because you can place more atoms
on the surface of the larger sphere), and the sum of all these minute
interactions decays at a slower rate than for the isolated two-atom case.
The electrostatic interaction energy, 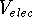 ,
between two non-bonded atoms i and j is usually
represented by Coulomb's law:
,
between two non-bonded atoms i and j is usually
represented by Coulomb's law:
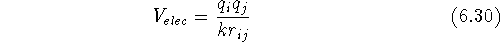
where 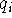 ,
, 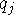 are the net atomic charges of atoms
i and j, respectively,
are the net atomic charges of atoms
i and j, respectively,
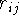 is the interatomic distance, and k is the dielectric constant
of the medium between the interacting charges
is the interatomic distance, and k is the dielectric constant
of the medium between the interacting charges . Some force fields use
the interaction of bond dipoles as an approximation to electrostatic
contribution.
Strictly speaking, Coulomb's law can only adequately describe the interaction
of two point charges in a continuous medium. In our case, however,
charges are not point charges and the medium is not continuous. For this
reason, the Coulomb's law in its original form is a crude approximation.
. Some force fields use
the interaction of bond dipoles as an approximation to electrostatic
contribution.
Strictly speaking, Coulomb's law can only adequately describe the interaction
of two point charges in a continuous medium. In our case, however,
charges are not point charges and the medium is not continuous. For this
reason, the Coulomb's law in its original form is a crude approximation.
The electrostatics
of molecules (especially macromolecules) is an important factor in their
biological function since it is responsible
for long-range inter- and intramolecular forces. These are large forces
compared to other interactions, e.g., the interaction energy of
two point charges -0.3 a.u. and +0.3 a.u., respectively,
separated by a distance of 10 Å in vacuum is
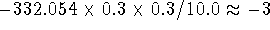 kcal/mol, i.e.,
very substantial for such a large separation between these modestly charged
atoms. For this reason,
the research in the area of adequate representation of molecular
electrostatics, yet computationally feasible, is very active.
There are methods which allow one
to incorporate polarizability, changes in dielectric constant (i.e., on the
protein/solution interface), etc., and these have proved to be very successful
in describing long range electrostatic interactions. However, these
methods are computationally expensive and for routine calculations
simplistic approximations are used.
The dielectric constant, k, is a well defined quantity only for
macroscopic systems. At the molecular level, a common approximation
is to use its value for a vacuum (i.e., k=1). To take into account
the presence of other atoms in the molecule or to incorporate the
influence of the solvent, different values are used in the range
between k=1 (vacuum) to k=80 (water). Another approach
is to assume that the
dielectric constant is proportional to the distance between
charges, usually in a linear fashion,
kcal/mol, i.e.,
very substantial for such a large separation between these modestly charged
atoms. For this reason,
the research in the area of adequate representation of molecular
electrostatics, yet computationally feasible, is very active.
There are methods which allow one
to incorporate polarizability, changes in dielectric constant (i.e., on the
protein/solution interface), etc., and these have proved to be very successful
in describing long range electrostatic interactions. However, these
methods are computationally expensive and for routine calculations
simplistic approximations are used.
The dielectric constant, k, is a well defined quantity only for
macroscopic systems. At the molecular level, a common approximation
is to use its value for a vacuum (i.e., k=1). To take into account
the presence of other atoms in the molecule or to incorporate the
influence of the solvent, different values are used in the range
between k=1 (vacuum) to k=80 (water). Another approach
is to assume that the
dielectric constant is proportional to the distance between
charges, usually in a linear fashion, 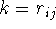 . This reflects the
fact that for distant charges there is a higher probability for other
atoms or solvent molecules (i.e., polarizable entities) to enter the
space between the two charges.
. This reflects the
fact that for distant charges there is a higher probability for other
atoms or solvent molecules (i.e., polarizable entities) to enter the
space between the two charges.
The major ambiguity, however, is with the concept of atomic charge itself.
The atom is made up of
a nucleus and electrons orbiting around it, and its charge is zero
by definition. However, in the molecule, averaged electron trajectories are
no longer centrosymmetric around nuclei, due to the formation of chemical bonds
between atoms, and the resulting average electron density can be a very
convoluted function in three dimensions.
Depending on atom electronegativity electrons are on average closer to more electronegative
atoms and farther from atoms with low electronegativity.
The net effect of
this unequal electron distribution can be approximated by placing
a number of point charges
in such a way that they reproduce the electrostatics of the
molecule with reasonable accuracy.
Usually, these charges are placed at the
positions of atomic nuclei and are called
net atomic charges.
electrons are on average closer to more electronegative
atoms and farther from atoms with low electronegativity.
The net effect of
this unequal electron distribution can be approximated by placing
a number of point charges
in such a way that they reproduce the electrostatics of the
molecule with reasonable accuracy.
Usually, these charges are placed at the
positions of atomic nuclei and are called
net atomic charges.
There are several ways of deriving atomic charges depending on
which molecular property is chosen to be represented best.
In many popular
force fields they are chosen to reproduce known
experimental data, e.g.: dipole moments, geometries, vibrational spectra, etc.
They are frequently derived theoretically from a variety of
electronegativity equalization schemes and quantum calculations at
different levels of sophistication. In the case of quantum
chemical calculations,
the charges may be derived either from population analysis or fitted by least
squares to the electrostatic potential. The charges
derived from ab initio electrostatic potential are considered superior
but this method is also the most computationally demanding.
The effect of hydrogen bonding is incorporated into the
potential energy surface
of a molecular system in a variety of ways.
In general, hydrogen bonds are formed
between hydrogen donor and hydrogen acceptor groups:
--D--H...A--AA--. The simplest approach, which at the
same time performs very well, is to assume that the bond between
hydrogen donor atom D and hydrogen atom H is polarized to the
extent that the electron density in the vicinity of the proton is negligible,
i.e., that the proton does not contribute to the
van der Waals energy. In this model (introduced by Hagler and coworkers),
the proton and the acceptor atom attract each another since they possess
opposing net charges. This results in the stretching of the
D--H bond and driving atom
A towards the hydrogen. Balance is achieved by contributions from
the D--H
stretching term, and electrostatic and van der Waals repulsions of atoms
D and A. This approach does not impose any directionality
on the hydrogen bonds but the balance of all of these
forces usually yiels a geometry close to linear (i.e., when atoms
D, H, A and AA lie on the straight line).
Some more elaborate models explicitly use powers of
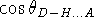 and
and
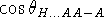 to enforce the linearity of the observed hydrogen
bond geometry and incorporate the
12-10 Lennard-Jones potential for the distance
between H and A.
to enforce the linearity of the observed hydrogen
bond geometry and incorporate the
12-10 Lennard-Jones potential for the distance
between H and A.
The last category of terms which appears in the potential energy function
is constraints. Their utility depends on the intended use of the
potential energy function and they will be described later in this chapter.
The individual energy terms differ in the magnitude of their contribution
to the total potential energy of the molecule. The bond stretching and
angle bending terms are considered ``hard'' terms, since even a small
distortion in the ``optimal'' value of bond length or valence angle produces
a very large positive contribution to the
potential energy. For this reason, the
variation in bond lengths and valence angles is usually negligible
in molecules without substantial strain. Larger variations are only
evident in strained ring systems or crowded molecules. In fact, the
overall shape of the molecule results from a balance between the
softer contributions,
i.e., torsional terms and non-bonded terms. It is therefore a common practice
to freeze bond lengths and valence angles at their optimal values and
consider only torsional and non-bonded interactions as the first approximation.


Next: Molecular Mechanics
Up: Molecular Modeling
Previous: Types of molecular images
Computational Chemistry
Wed Dec 4 17:47:07 EST 1996
 hybridized
carbon atoms is around 1.5 Å long and the valence angle for an
sp3 carbon is
usually close to 109
hybridized
carbon atoms is around 1.5 Å long and the valence angle for an
sp3 carbon is
usually close to 109  . On the other hand, these values are frequently
distorted in some strained ring systems (like cyclopropane) or
crowded molecules (like tetramethylmethane). The concept of molecular
strain can be imagined as if bonds were elastic springs whose distortion
is reflected by a positive increment (i.e., thermodynamically
unfavorable) to the potential energy of the molecule.
These approaches were originally called empirical potential energy
functions but the term molecular mechanics is now in common use.
The mathematical form of this
potential energy function (also called potential energy surface) is:
. On the other hand, these values are frequently
distorted in some strained ring systems (like cyclopropane) or
crowded molecules (like tetramethylmethane). The concept of molecular
strain can be imagined as if bonds were elastic springs whose distortion
is reflected by a positive increment (i.e., thermodynamically
unfavorable) to the potential energy of the molecule.
These approaches were originally called empirical potential energy
functions but the term molecular mechanics is now in common use.
The mathematical form of this
potential energy function (also called potential energy surface) is:
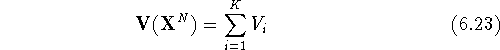
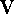 represents the potential
energy of the molecular system and depends upon the cartesian coordinates
of all atoms denoted here as
represents the potential
energy of the molecular system and depends upon the cartesian coordinates
of all atoms denoted here as 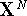 .
. 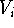 's are individual energy terms
representing contributions from individual interactions which
depend upon the cartesian coordinates of partaking atoms.
Having
's are individual energy terms
representing contributions from individual interactions which
depend upon the cartesian coordinates of partaking atoms.
Having 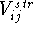 , for a covalent bond between atoms
i and j, represents a contribution to the potential energy
resulting from deformation of the optimal bond length. Most frequently a simple
symmetric parabola (i.e., harmonic approximation) is used:
, for a covalent bond between atoms
i and j, represents a contribution to the potential energy
resulting from deformation of the optimal bond length. Most frequently a simple
symmetric parabola (i.e., harmonic approximation) is used:
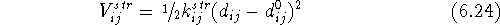
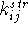 is a bond stretching parameter (frequently called
a bond stretching force constant) and its value represents the stiffness
of the bond (i.e., the ease with which the bond can be distorted). Large
values of
is a bond stretching parameter (frequently called
a bond stretching force constant) and its value represents the stiffness
of the bond (i.e., the ease with which the bond can be distorted). Large
values of 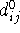 corresponds
to the optimal (i.e., unstrained) bond length. Contribution
from this term is never negative and is equal to zero only when the actual bond
length,
corresponds
to the optimal (i.e., unstrained) bond length. Contribution
from this term is never negative and is equal to zero only when the actual bond
length, 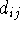 , is exactly equal to the optimal bond length
, is exactly equal to the optimal bond length 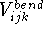 , is represented by a
harmonic expression depending upon the bending force constant,
, is represented by a
harmonic expression depending upon the bending force constant,
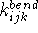 , the actual value of the valence angle
, the actual value of the valence angle 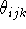 and its
``natural'', optimal value,
and its
``natural'', optimal value, 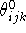 :
:
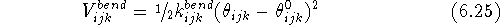
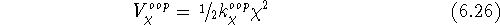
 hybridized carbon,
hybridized carbon, 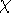 is an angle between
one of the bonds originating at the central atom and a plane passing through
the other two bonds.
is an angle between
one of the bonds originating at the central atom and a plane passing through
the other two bonds.
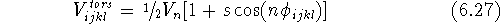
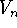 is the height of the torsional barrier; s is -1 if a minimum
occurs for the eclipsed conformation and +1 if a minimum corresponds to
the staggered conformation; n is a periodicity, i.e., the number of maxima
per full revolution; and
is the height of the torsional barrier; s is -1 if a minimum
occurs for the eclipsed conformation and +1 if a minimum corresponds to
the staggered conformation; n is a periodicity, i.e., the number of maxima
per full revolution; and 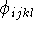 is a torsional angle.
For the torsional angle involving C--C bond in ethane, s=1 and n=3, while
for the double bond in ethylene s=-1 and n=2. More elaborate
force fields use as a torsional term the sum of several cosine functions
with different periodicities to account for smaller ``humps'' appearing
on the torsional energy dependence. On occasion, the harmonic potential
is used for torsional angles around double bonds due to their stiffness.
is a torsional angle.
For the torsional angle involving C--C bond in ethane, s=1 and n=3, while
for the double bond in ethylene s=-1 and n=2. More elaborate
force fields use as a torsional term the sum of several cosine functions
with different periodicities to account for smaller ``humps'' appearing
on the torsional energy dependence. On occasion, the harmonic potential
is used for torsional angles around double bonds due to their stiffness.

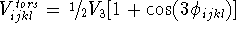 .
.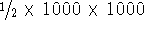 pairwise
interactions,
or
pairwise
interactions,
or 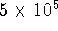 terms. The
terms. The 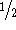 factor
comes from the fact that each pair is included only once, i.e., the pair
i--j is equivalent to j--i. For the three-body potentials
we would have to calculate interaction for each possible combination of
three atoms (excluding valence angles), i.e., close to
factor
comes from the fact that each pair is included only once, i.e., the pair
i--j is equivalent to j--i. For the three-body potentials
we would have to calculate interaction for each possible combination of
three atoms (excluding valence angles), i.e., close to
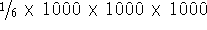 or
or
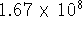 terms! For that reason, the three-body potentials
are not routinely calculated. However, even two-body potentials are
computationally demanding and approximations are used.
The large number of terms is frequently
reduced by omitting the
interactions of distant atoms (i.e., skipping calculation
of the non-bonded term for atoms which are further apart than some
predetermined
cut off distance). However, checking if atoms are outside the cut off distance
is also a substantial computational effort for larger molecules.
terms! For that reason, the three-body potentials
are not routinely calculated. However, even two-body potentials are
computationally demanding and approximations are used.
The large number of terms is frequently
reduced by omitting the
interactions of distant atoms (i.e., skipping calculation
of the non-bonded term for atoms which are further apart than some
predetermined
cut off distance). However, checking if atoms are outside the cut off distance
is also a substantial computational effort for larger molecules.

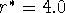 Å,
Å, 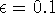 kcal/mol,
kcal/mol,
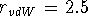 Å
Å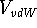 , is composed
of two terms opposing each another, a repulsive term
, is composed
of two terms opposing each another, a repulsive term 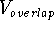 , and
an attractive term,
, and
an attractive term, 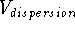 :
:
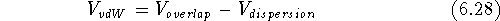
 :
:
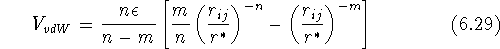
 is the depth of a well (i.e., the maximal attraction energy),
n and m are exponents (typically n=12 or 9, and m=6),
and
is the depth of a well (i.e., the maximal attraction energy),
n and m are exponents (typically n=12 or 9, and m=6),
and  is the distance between atoms which corresponds to a minimum.
As you can see from Fig.
is the distance between atoms which corresponds to a minimum.
As you can see from Fig. 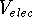 ,
between two non-bonded atoms i and j is usually
represented by Coulomb's law:
,
between two non-bonded atoms i and j is usually
represented by Coulomb's law:
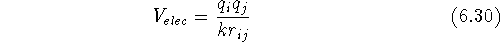
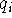 ,
, 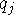 are the net atomic charges of atoms
i and j, respectively,
are the net atomic charges of atoms
i and j, respectively,

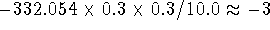 kcal/mol, i.e.,
very substantial for such a large separation between these modestly charged
atoms. For this reason,
the research in the area of adequate representation of molecular
electrostatics, yet computationally feasible, is very active.
There are methods which allow one
to incorporate polarizability, changes in dielectric constant (i.e., on the
protein/solution interface), etc., and these have proved to be very successful
in describing long range electrostatic interactions. However, these
methods are computationally expensive and for routine calculations
simplistic approximations are used.
The dielectric constant, k, is a well defined quantity only for
macroscopic systems. At the molecular level, a common approximation
is to use its value for a vacuum (i.e., k=1). To take into account
the presence of other atoms in the molecule or to incorporate the
influence of the solvent, different values are used in the range
between k=1 (vacuum) to k=80 (water). Another approach
is to assume that the
dielectric constant is proportional to the distance between
charges, usually in a linear fashion,
kcal/mol, i.e.,
very substantial for such a large separation between these modestly charged
atoms. For this reason,
the research in the area of adequate representation of molecular
electrostatics, yet computationally feasible, is very active.
There are methods which allow one
to incorporate polarizability, changes in dielectric constant (i.e., on the
protein/solution interface), etc., and these have proved to be very successful
in describing long range electrostatic interactions. However, these
methods are computationally expensive and for routine calculations
simplistic approximations are used.
The dielectric constant, k, is a well defined quantity only for
macroscopic systems. At the molecular level, a common approximation
is to use its value for a vacuum (i.e., k=1). To take into account
the presence of other atoms in the molecule or to incorporate the
influence of the solvent, different values are used in the range
between k=1 (vacuum) to k=80 (water). Another approach
is to assume that the
dielectric constant is proportional to the distance between
charges, usually in a linear fashion, 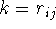 . This reflects the
fact that for distant charges there is a higher probability for other
atoms or solvent molecules (i.e., polarizable entities) to enter the
space between the two charges.
. This reflects the
fact that for distant charges there is a higher probability for other
atoms or solvent molecules (i.e., polarizable entities) to enter the
space between the two charges.
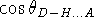 and
and
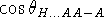 to enforce the linearity of the observed hydrogen
bond geometry and incorporate the
12-10 Lennard-Jones potential for the distance
between H and A.
to enforce the linearity of the observed hydrogen
bond geometry and incorporate the
12-10 Lennard-Jones potential for the distance
between H and A.