Lone Pairs and the Molecular Electrostatic Potential of Water**
David Young
James F. Harrison*
[*] Mr. D. Young, Prof. J. F. HarrisonDepartment of Chemistry and Center for Fundamental
Materials Research
Michigan State University
East Lansing, MI 48824-1322
FAX: (517) 353-1793
[**] A National Science Foundation sponsored Research
Experience for Undergraduates Fellowship is
gratefully acknowledged.
E-mail
David Young
at dyoung@asc.edu
E-mail
James F. Harrison
at harrison@cemvax.cem.msu.edu
Note about graphics
If you do not have any graphics display capability, this text should still be readable, but you may not get as much out of the paper because we use visualization techniques as our data analysis method.
Abstract
The model of lone pair electrons is an extremely important and useful tool and yet the nature of these lone pair electrons remains elusive. In this paper we examine the electron density and electrostatic potential around the water molecule using ab initio electronic structure techniques. Scientific visualization is used to examine the behavior of these observables in the region to the "rear" of the water molecule, where electron lone pairs are depicted. We find that the electron density exhibits no significant structure which might indicate the presence or location of electron lone pairs. However, the electrostatic potential reveals more structure and exhibits two minima in the regions where tetrahedrally arranged lone pairs would be expected.
Lone pairs in water and related systems are frequently described as being regions of enhanced electron density.[1] Indeed, the familiar "rabbit ears" representation[2] (the equivalent orbital or EO scheme) epitomizes this idea and allows the systemization and rationalization of many chemical properties.
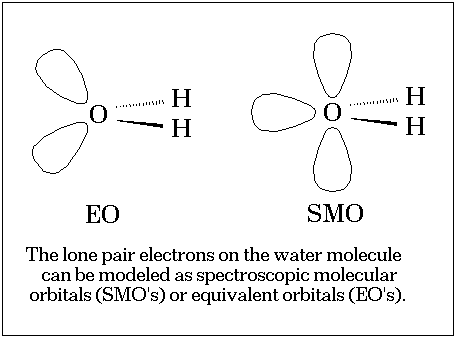
However, in spite of the enormous appeal and success of this representation little is known about the physical nature of the lone pairs. Most discussions[3] invoke the molecular orbital model and focus on the nature of individual orbitals and since these orbitals are not unique[4] these discussions are somewhat subjective. In this communication we explore the concept of the lone pairs in an isolated, gas phase water molecule by focusing on two invariants of the water wavefunction: the electron density[5] and the molecular electrostatic potential, MEP[6] derived from this density.
When we examine the electron density we will be looking at the electron distribution to the "rear" of the oxygen (in the "lone pair" region) to see if variations in this distribution support the idea of the lone pairs being regions of enhanced electron density. Additionally, we will calculate the MEP surrounding the water molecule and we will identify those regions in which it is most negative. These negative regions are the natural destination of an incoming infinitesimal positive point charge and it is interesting to know if these regions of low MEP coincide with our intuition about the location of the lone pairs.
The electron density and the electrostatic potential have been calculated from high quality ab initio wavefunctions at the self consistent field (SCF)[4] and configuration interaction (CI)[4] level. The oxygen atom was described by a Duijenveldt[7] 11s 7p basis contracted to 5s 5p along with three uncontracted d primitives[8] with exponents of 2.25, 0.75 and 0.25. The hydrogen atom is the Dunning[9] 4s, contracted to 2s with a single p function with an exponent of 1. The SCF total energy of -76.06160H and the CI total energy of -76.34446H compare favorably with previous calculations[8] which predict, at best, -76.06429H for the SCF total energy and -76.35328H for the CI total energy. The optimized geometries used were a bond length of 0.955Å and a bond angle of 105.1degrees. for the CI wavefunction and a length of 0.942Å and angle of 106.2degrees. for the SCF wavefunction. The experimental geometry is a bond length of 0.959Å and an angle of 103.9degrees.[10]. The reported results were obtained with the CI wavefunction but we find essentially the same results using the SCF function. The calculations were performed using the Columbus[11] and Gaussian 90[12] programs and the subsequent visualizations used the Advanced Visualization System (AVS)[13]. We feel confident our results will survive future inevitable improvements in the accuracy of the computed electron density.
In figure 1 we show two views of the electron density in the water molecule. On the left we contour the density in the molecular plane and on the right, in the plane perpendicular to this plane and bisecting the HOH angle. The innermost contour corresponds to 0.142 e/Å3 and subsequent contours decrease uniformly by 5.70 x 10-3 e/Å3. Clearly, the electron density is rather featureless, especially in the lone pair region. Figure 2 shows a sequence of three dimensional isosurfaces of the density beginning at 0.148 e/Å3 and decreasing to 0.00148 e/Å3. We see that contour levels 0.148 and 0.074 e/Å3 represent density essentially localized on oxygen with the hydrogens beginning to contribute at 0.0592 e/Å3. By the time we get to the contour level 0.00148 e/Å3 we have a rather structureless electron distribution. The size of this last surface is, at most, 3.23 Å across.
Although the density is featureless, it is not spherical in the lone pair region. Figure 3 shows the 0.0327 e/Å3 isosurface with an inscribed sphere centered about the O atom. The inscribed sphere is colored green and has been increased in size until it just breaks through the isosurface. If the isosurface was equidistant from the oxygen, the inscribed sphere would break the surface at all points simultaneously. Consequently the white areas are further from the nucleus than the green areas. If we increase the radius of the inscribed green sphere very slightly we see the green sphere completely outside of the isosurface. The electron distribution is very nearly spherical and we see no pronounced variation in the electron density that reminds us of the lone pairs. Note that the ragged line where the sphere meets the density isosurface is due to the visualization software approximating a sphere by a high order polygon. However, the slight asymmetry in the electron distribution, as shown in figure 3, is indeed consistent with the notion of lone pairs oriented approximately tetrahedrally with respect to the OH bonds.
The MEP is an observable, intimately related to the electron density. A point particle with an infinitesimally small charge q will have an energy given by the product of q and the value of MEP at the point of interest. There are regions around the water molecule where is positive and regions where it is negative. Positive point charges will be attracted to the regions of negative potential and negative charges to the regions of positive potential.
We have evaluated the MEP using the same electron density function contoured in figures 1-3 and in figure 4 we show contours of the MEP in the molecular plane and in the plane bisecting the HOH angle. There are several interesting observations to be made. First, we see that the negative contours are clustered to the rear of the water molecule away from the positive hydrogens. Secondly, there is considerable structure in the MEP and while there are minima in both planes the global minima are in the plane bisecting the HOH angle. These two regions are symmetrically located above and below the plane containing the nuclei, are 1.26 Å from the oxygen nucleus and subtend an angle of 98 with the oxygen. Figure 5 shows the three dimensional nature of these regions of low electrostatic potential. The contour values are given in energy units (eV), which corresponds to the energy a unit positive charge would have at these points. The -1.90 eV contour encloses a volume which extends continuously from one side of water to the other. At -1.97 eV we see the regions beginning to separate and at -2.04 eV the minima in the MEP are symmetrically arranged above and below the molecular plane. The absolute minimum in the MEP is approximately -2.27 eV at which value the enclosed volumes are zero. Figure 6 shows a positive value of the MEP in blue (+27.2 eV) and a negative region in yellow (-2.041 eV). These minima define directions in space not to dissimilar to those associated with the approximately tetrahedrally located lone pairs often associated with water.
These results suggest that it might be fruitful and more physically accurate to consider the lone pairs in water as a derived property of the electron density, e.g., the MEP rather then as the electron density itself. While the concept of a lone pair is extraordinarily valuable in interpreting, predicting and systematizing many aspects of chemistry, its characterization, as regions of space with significantly enhanced electron density is a considerable oversimplification. Indeed, as we have shown, lone pairs (at least in water) correspond to regions of minimum electrostatic potential rather than regions of enhanced electron density.
Literature Cited:
1. D. Eisenberg, W. Kauzmann, The Structure and Properties of Water, Oxford University Press, 1969.
2. See for example any text that discusses the VSEPR theory of molecular geometry. A representative one being, P. W. Atikins, J. A. Beran, General Chemistry, Scientific American Books, 1992.
3. R. B. Martin, J. Chem. Educ. 1988, 65, 668-670; M. J. Laing, ibid. 1987, 64, 124-128.
4. I. N. Levine, Quantum Chemistry, Allyn and Bacon, 1983.
5. Vedene H. Smith in Electron Distributions and the Chemical Bond, (Eds: P. Coppens and M. B. Hall), Plenum, 1981, p. 3.
6. P. Politzer, J. S. Murray in Transactions of the American Crystallographic Association, Vol. 26 (Ed: R. Blessing) 1990, p. 23.
7. F. B. van Duijneveldt, IBM Research Report RJ 945 1971.
8. R. R. Lucchese, M. P. Conrad, H. F. Schaefer, III J. Chem. Phys., 1978, 68, 5292-5294.
9. T. H. Dunning, Jr., P. J. Hay in Methods in Molecular Electronic Structure Theory, Ed: H. F. Schaefer, III, Plenum, 1977.
10. D. J. Defrees, B. A. Levi, S. K. Pollack, W. J. Hehre, J. S. Binkley, J. A. Pople J. Am. Chem., Soc. 1979, 101, 4085.
11. R. Shepard, I. Shavitt, R. M. Pitzer, D. C. Comeau, M. Pepper, H. Lischka, P. G. Szalay, R. Ahlrichs, F. B. Brown, J. G. Zhao. Internat. J. Quantum Chem., 1988, S22, 149-165.
12. J. J. Frisch, M. Head-Gordon, G. W. Trucks, J. B. Foresman, H. B. Schlegel, K. Raghavachari, M. Robb, J. S. Binkley, C. Gonzales, D. J. Defrees, D. J. Fox, R. A. Whiteside, R. Seeger, C. F. Melius, J. Baker, R. L. Martin, L. R. Kahn, J. J. P. Stewart, S. Topiol, J. A. Pople Gaussian 90, Revision J, Gaussian, Pittsburgh, 1990.
13. AVS, Advanced Visualization Systems: Waltham, 1992.
Figure Captions:
Figure 1
Two views of the electron density in the water molecule.The electron density is contoured both in the molecular plane and perpendicular to the molecular plane bisecting the HOH angle. The innermost contour corresponds to 0.142 e/Å3 and the subsequent contours decrease uniformly by 0.00570 e/Å3.
This data can also be colorized to produce an image of the electron density in the molecular plane or perpendicular to the molecular plane or both.
Figure 2
Three dimensional isosurfaces of the electron density begining at 0.148 e/Å3 and decreasing to 0.00148 e/Å3.
Figure 3
The 0.0327 e/Å3 isosurface with an inscribed sphere (green) centered at oxygen. The radius of the inscribed sphere is just large enough to break through the isosurface.
Figure 4
Two views of the electrostatic potential of the water molecule.The electrostatic potential is contoured both in the molecular plane and perpendicular to the molecular plane
This data can also be colorized to produce an image of the electrostatic potential in the molecular plane or perpendicular to the molecular plane or both. Here we have made two passes through the spectrum, one for the positive values and one for the negative values. This creates a sharp transition from dark to light where the node is.
Figure 5
Three dimensional nature of regions of low electrostatic potential.
Figure 6
The molecular electrostatic potential (MEP) in water. The blue surface corresponds to a MEP of +27.2 eV while the yellow surface corresponds to a MEP of -2.041 eV.
